0x01a: The Diffie-Hellman Protocol & Its Mathematical DLP Analysis

[ DESCRIPTIVE REFERENCE ]

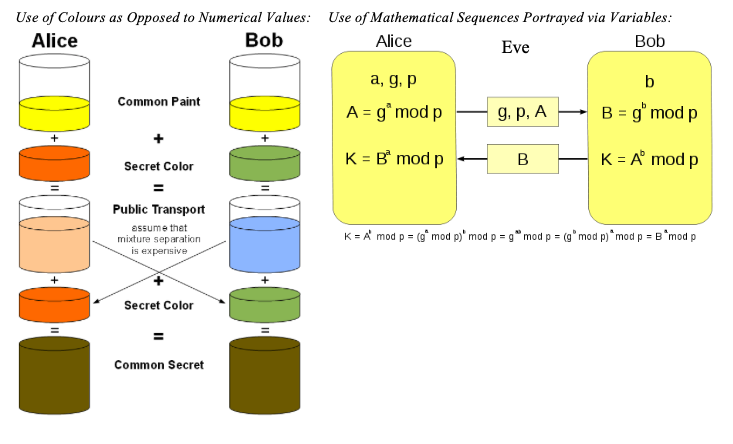
Diffie–Hellman key exchange was one of the first public-key protocols as originally conceptualized by Ralph Merkle and named after Whitfield Diffie and Martin Hellman. Traditionally, secure encrypted communication between two parties required that they first exchange keys by some secure physical channel, such as paper key lists transported by a trusted courier. The D-H protocol therefore provides a secure alternative to jointly establish a shared secret key over an insecure channel.

[ PICTORIAL REPRESENTATION ]

Where m is Alice's private key, and mG is her public key. And where n is Bob's private key, and nG is his public key.

[ ANALYSIS ]

As described above, the Diffie-Hellman key exchange is a means of generating a shared secret between two individuals (i.e. Alice and Bob) without it being known to external ‘observers’/‘listeners’ on the communication channel (i.e. Eve) even though a large portion of exchanged data that generated the shared secret is known. The D-H key exchange is not encryption, but a foundation to public key/asymmetric cryptography.

The resulting shared secret devised via D-H key exchange is never saved, nor is it transmitted or made visible by any means. The descriptive term of this is known as Forward Secrecy (FS), which usually exists as a successor product derived from the use of non-deterministic algorithms. The non-deterministic algorithm incorporated within the D-H protocols generates trap-door functions, which in return facilitates what is known as the discrete logarithm problem. This means, that it’s easy to mathematically compute the shared secret one-way, but incredibly difficult to reverse the computation to determine the initial secret values, especially if the shared numerical secret is a large number (as later demonstrated).

[ THE MECHANICS ]

0x01:
A prime value (p) and a primitive root modulo generator (g) are devised, and shared publicly between Alice and Bob. These values are referred to as public parameters or public values.

0x02:
Alice and Bob then both randomly select their private/secret value, a (Alice’s), and b (Bob’s) of which is only known to themselves.

0x03:
Alice computes A = ga mod p and sends the result of A publicly to Bob

0x04:
Likewise, Bob incurs the same process and computes B = gb mod p and sends the result of B publicly to Alice.

0x05:
Alice then takes the computational value of Bob’s public result, B and raises it to the power of her private value a and, therefore, solves S = Ba mod p, where S is the shared secret.

0x06:
Likewise, Bob performs the same operation with Alice’s public computed result, A, by raising it to the power of his private number b and, therefore, solves S = Ab mod p, where S is the shared secret.

A common shared secret between Alice and Bob has now been devised in secrecy, where the value computed in step 0x05 is identical to the resulting computed value in step 0x06). The resulting value is the same despite using different orders of exponentiation.

We can understand, with further mathematical analysis, as to how Alice and Bob both received the same value, being S, via different variable computations. This is achievable via the existing properties of modular arithmetic exponents. Of which is that, the resulting computed values are identical to each other despite the order of the calculated exponentiation:

$$\color{#20c20e}(g^a\textit{ mod p)}^b\textit{ mod p} \cong g^{ab}\textit{ mod p} \cong (g^b\textit{ mod p})^a\textit{ mod p} = g^{ba}\textit{ mod p}$$

[ DEMONSTRATION WITH SMALL NUMERICAL VALUES ]

For demonstration purposes, small numerical values have been used. These given values are as follows:

Prime modulus (p) = 17,		
Primitive root modulo generator (g) = 3,
Alice’s private value (a) = 15,	
Bob’s private value (b) = 13

Alice’s Public Value (A) is computed via:

$$\color{#20c20e}3^{15}\textit{ mod 17} = 6 \textit{ }(A = g^a \textit{ mod p})$$

Bob’s Public Value (B) is computed via:

$$\color{#20c20e}3^{13}\textit{ mod 17} = 12 \textit{ }(B = g^b \textit{ mod p})$$

And now the exchange, Alice computes the shared secret (S) via:

$$\color{#20c20e}12^{15}\textit{ mod 17} = 10 \textit{ }(S = B^a \textit{ mod p})$$

Bob Computes the shared secret (S) via:

$$\color{#20c20e}6^{13}\textit{ mod 17} = 10 \textit{ }(S = A^b \textit{ mod p})$$

The shared secret (S) is now devised between Alice and Bob, in this case, being 10’.

At it’s initial appearance, it may not seem like it, but Alice and Bob did the same calculation:

$$\color{#20c20e}12^{15}\textit{ mod 17 } \cong 6^{13}\textit{ mod 17 } \cong 6^{13}\textit{ mod 17 }\textit{ }(S = B^a\textit{ mod p} \cong S = A^b \textit{ mod p)}$$

For example, considering Alice, the value ‘12’ that she received from Bob (B) was calculated via 12 = 3¹³ mod 17. Therefore her calculation is the same as:

$$\color{#20c20e}(3^{13})^{15} \textit{mod 17 } \cong 3^{13*15} \textit{mod 17}$$

For example, considering Bob, the value ‘6’ that he received from Alice (A) was calculated via: 6 = 3¹⁵ mod 17. Therefore, his calculation is the same as:

$$\color{#20c20e}(3^{15})^{13} \textit{mod 17 } \cong 3^{15*13} \textit{mod 17}$$

Which means, these two equations are congruent to each other:

$$\color{#20c20e}(g^b\textit{mod p})^a \textit{mod p} = g^{ba}\textit{mod p} \cong (g^b\textit{mod p})^a\textit{mod p} = g^{ba} \textit{mod p}$$

$$\color{#20c20e}\therefore (3^{13} \textit{mod 17})^{15} \textit{mod 17 } = 3^{13*15} \textit{mod 17} \cong (3^{15} \textit{mod 17})^{13} \textit{mod 17 } = 3^{15*13} \textit{mod 17}$$

So Alice computes the value in one order, and Bob computes it in the other. Alice never knows Bob’s secret value used to calculate the result, nor does Bob ever know Alice’s used secret value yet both Alice and Bob arrive with the same resulting value. We can be confidently certain that neither Eve nor anybody else but Alice and Bob know the generated secret key. This secret key can now be used as a cryptographic encryption key for any encryption algorithm that incorporates shared secrets to parse mathematical functions that alter original plaintext to the corresponding cipher text and vice versa according to the mathematical ‘rules’ associated/devised with the secret key’s value.

Eve’s Observations if Intercepting the Public Channel’s Data Traffic During the Exchange

The values transmitted publicly via an insecure channel are: 6 (A), 12 (B), 3 (g), and 17(p). Depending on the size of the values, particularly the prime modulus (p), without one of the private/secret values, 15 (a) or 13 (b), Eve will be unable to solve the resulting shared secret solution (S). However, as stated above, small number values have been incorporated for demonstration purposes. These values are much larger in a real world-simulating environment which in turn enhances the impracticality to solve S without a, or, b via reverse mathematics. This leads to the discrete logarithm problem.

[ THE DISCRETE LOGARITHM PROBLEM ]

The discrete logarithm problem associated with the Diffie-Hellman key exchange is as follows:

$$\color{#20c20e}\textit{"Given y, find x so that g x mod p = y"}$$

With small values, it’s quite simple:

329 mod 17 = 12 (easy trap-door function)
3x mod 17 = 12 (harder to reverse but not difficult. It’s just a matter of trial and error)

With large values, it becomes computationally intractable:

Suppose the prime modulus p has a length of 1024-bits (~ 308 base10 digits), with x being known this is a simple trap-door function. However, without knowing x, p, being 1024-bits in length, is a value so large that it means there are 2¹⁰²⁴ possible combinations for x.

While such a discrete logarithm problem is traditionally used (g^x mod p), the general process of the D-H key exchange can be modified to use elliptic curve cryptography (ECC) to form the Elliptic Curve Diffie-Hellman key exchange protocol (ECDH). A similar analysis on the ECDH protocol and its mathematical DLP can be observed here.

[ PYTHON IMPLEMENTATION FOR DEMONSTRATION ]

1	# Variable Declaration
2	sharedPrime = 23    # p  
3	sharedBase = 5      # g  
4	   
5	aliceSecret = 6     # a  
6	bobSecret = 15      # b  
7	   
8	# Begin
9	print('Publicly Shared Variables:')  
10	print('Publicly Shared Prime:', sharedPrime)  
11	print('Publicly Shared Base:', sharedBase)  
12	   
13	# Alice Sends Bob A = g^a mod p  
14	A = (sharedBase**aliceSecret) % sharedPrime  
15	print('\n Alice Sends Over Public Chanel:', A)  
16	   
17	# Bob Sends Alice B = g^b mod p  
18	B = (sharedBase ** bobSecret) % sharedPrime  
19	print('Bob Sends Over Public Chanel:', B)  
20	   
21	print( '\n------------\n')  
22	print('Privately Calculated Shared Secret:')  
23	  
24	# Alice Computes Shared Secret: s = B^a mod p  
25	aliceSharedSecret = (B ** aliceSecret) % sharedPrime  
26	print('Alice Shared Secret:', aliceSharedSecret)  
27	   
28	# Bob Computes Shared Secret: s = A^b mod p  
29	bobSharedSecret = (A**bobSecret) % sharedPrime
30	print('Bob Shared Secret:', bobSharedSecret) 

[ BREAKING DOWN THE SOURCE ]

Initially, a sum of four variables is defined, each containing unique data (in this case, integers). These variables are named sharedPrime, sharedBase, aliceSecret and bobSecret.

Each of these variables have been co-signed with single letters to later demonstrate the D-H mathematical functions for better understanding.

1	sharedPrime = 23    # p  
2	sharedBase = 5      # g  
3	aliceSecret = 6     # a  
4	bobSecret = 15      # b 

First Alice and Bob agree on a Prime number, sharedPrime (p) that must be a prime number. Likewise a base, sharedBase (g), is also agreed upon where g must be a primitive root modulo. These above mentioned values of 23 (p) and 5 (g) are public, and can therefore be known to anyone, such as Eve. Following these public values, Alice and Bob each randomly select their own unique private integer that they keep secret to themselves. Alice’s value: a is 6, Bob’s value: b is 15.

Alice’s public value (A) is computed via modular arithmetic:

16	A = (sharedBase**aliceSecret) % sharedPrime   #(A = g^a mod p) 

Which is the equivalent to A = 5⁶ mod 23, which = 8

This computed value is then printed to mimic it being transmitted over a public/insecure channel medium to Bob.

Likewise, Bob’s public value (B) is computed via modular arithmetic:

20	B = (sharedBase**bobSecret) % sharedPrime    #(B = g^b mod p) 

Which is the equivalent of B = 5¹⁵ mod 23, which = 19

This computed value is then also printed to mimic it being transmitted over a public channel medium to Alice.

Alice then computes the received value via:

27	aliceSharedSecret = (B**aliceSecret) % sharedPrime           #(S = B^a mod p) 

Which is the equivalent of S = 19⁶ mod 23, which = 2

Likewise, Bob does the same for the received value from Alice:

31	bobSharedSecret = (A**bobSecret) % sharedPrime 			#(S = A^b mod p) 

Which is the equivalent of S = 8¹⁵ mod 23, which = 2

Therefore, the shared secret, being 2, is now known to both Alice and Bob. Eve has no way of knowing it even though Eve knows values p, g, A and B (as displayed under the ‘Publicly Shared Variables’ output).

[ FINAL COMMENTS ]

The above implementation successfully demonstrates an accurate representation that exhibits how the D-H key exchange mechanism works by the properties of its mathematical functions.

For this implementation to contain a higher level of accuracy, the following must be considered:

1.  Instead of the public values being printed to mimic/simulate public transmission, 
    the values would actually be transmitted across a public channel. The implementation 
    would therefore be required to function on the Network Layer.

2.  Instead of using small numerical values, the use of extremely large numerals would 
    be incorporated. This would enhance the shared secret key’s integrity due to 
    Diffie-Hellman’s Key Exchange trap-door function. 

3.  The shared secret key should never be printed, saved or transmitted, and would 
    remain as a non-public secret. 

4.  Likewise, the same rule above applies for both Alice and Bob’s randomly devised 
    secret value.

5.  The secret should also never be derived directly. Typically, in a real-world 
    simulation the secret result is parsed through hash functions to produce a 
    corresponding hashed key. 

6.  Instead of the implementation selecting the private values statically via the 
    program’s source-code, it would instead generate these private values (each of Alice and Bob) 
    via a generator function that can either be devised, or imported.

7.  Additionally, during the random value generation, the implementation would incorporate 
    the use of a true-random number generator to enhance entropy (a measure of uncertainty) of
    the random values.